Metrics

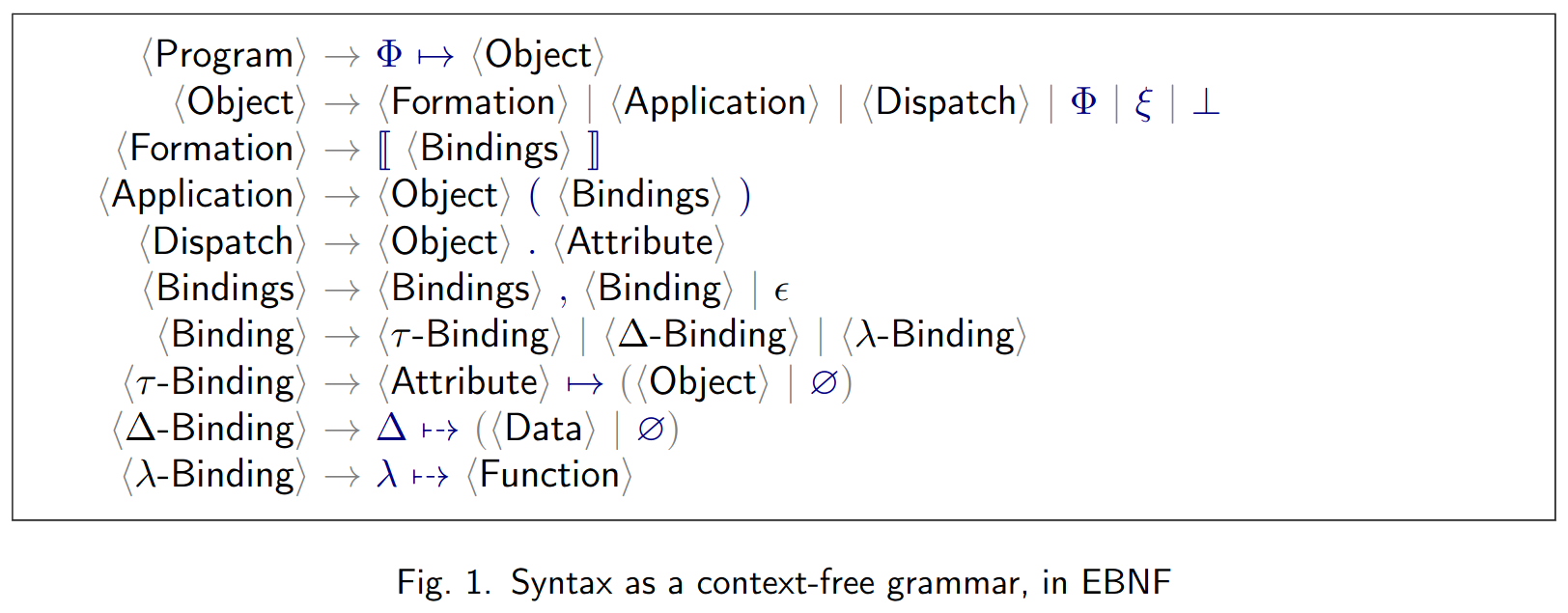
PHI grammar

We count

• Object formations
• Object applications
• Dynamic dispatches
• Dataless formations

Object formations

• Example: ⟦ d ↦ ∅, c ↦ ∅ ⟧

Object applications

• Example: ξ.b(c ↦ ⟦ ⟧)

Dynamic dispatches

• Example: ξ.ρ.c

Dataless formations

Definition: \( \Delta \)-depth

\( \Delta \)-depth of an object describes how deep data is in the object when recursively traversing values attached to the object attributes. That is, \( \Delta \)-depth is \( \infty \) for all objects except formations. More specifically:

1. the \( \Delta \)-depth of a formation with bytes attached to a \( \Delta \)-attribute is \( 1 \);
2. for a non-empty formation, the \( \Delta \)-depth is:
   1. \( 1 + M \), where \( M \) is the minimal depth among objects attached to attributes of this formation;
   2. \( \infty \) if there are no objects attached to attributes of this formation;
3. otherwise, the \( \Delta \)-depth of an object is \( \infty \).

Definition: Dataless object

An object is dataless if its \( \Delta \)-depth is greater than 2.

Examples

The following table demonstrates objects with their \( \Delta \)-depths:

CLI command

See normalizer metrics.